【ポケモンAI】モンテカルロCFRでナッシュ均衡を求める
続き。
前回はpoke_envという対戦シミュレーションライブラリと、CFR(Counterfactual Regret)というアルゴリズムを組み合わせて、1v1シングルバトルにおける最善手を計算してみた。
前回時点では手始めに片側プレイヤー視点での最善手のみ計算したが、今回はいよいよ双方向での計算を行う(行った)。つまり、両プレイヤーがお互いに戦略を最適化しながら均衡解を求める。ゲーム理論の用語でナッシュ均衡という。
今回の対戦メンツはこちらである。

ローブシン Lv.100 @命の珠
てつのこぶし
いじっぱり
H252 D252 S4
・れいとうパンチ
・まもる

フェローチェ Lv.100 @命の珠
ビーストブースト
いじっぱり
A252 S252 D4
・みがわり
・とんぼ返り
・どくづき
(ダメージ計算)
・アームハンマー 80.8 ~ 100.0 %
・れいとうパンチ 85.5 ~ 100.7 %
・マッハパンチ 33.9 ~ 39.9 %
・とびひざげり 80.0 ~ 94.2 %
今回はお互い単純に最大ダメージの技が最善手になってしまうと面白くないので、少し複雑な対面にした。攻撃技・まもる vs とびひざげり・みがわり の読み合い要素がある。
| れいとうパンチ | まもる | |
| とびひざげり | ○(先制で大ダメージ) | ✕ (HP -50%) |
| みがわり | ✕ (HP -25%) | ○(身代わりを残せる) |
つまりお互いの最善手は、相手の行動に左右されることになる。必勝法は存在しない。このような局面において、CFRアルゴリズムが直近の相手の戦略に応じて最適な戦略を計算し、いずれ収束(均衡)に至るかどうか、試した。
やったこと
シミュレーション対戦のルール設定:
(Pokemon Showdownの[Gen 8 1v1]ルールを使用)
・第8世代環境
・1vs1シングルバトル
・ダイマックスは禁止
・お互いレベル100
モンテカルロCFRの設定 (太字は前回からの変更点)
・両プレイヤーで後悔の計算、戦略の更新を行う
・探索率=0.6
・100000回の繰り返し
・情報集合はshowdownサーバーから送られてくる対戦メッセージをそのまま使用する
結果1: 繰り返しごとの勝率推移
最終的な戦略だけ見ても人間も正解はわからないし、「本当に学習しているのか?」という疑問があったので、勝率計算をしてとりあえず計算がうまくいっていることを確認した。
プレイヤー1、プレイヤー2それぞれ、以下のような仮想プレイヤーと戦わせて勝率を計算している。
- ランダムにコマンド選択するプレイヤー(RandomPlayer) →図の青線
- 最大ダメージの技のみを選択するプレイヤー(MaxDamagePlayer) →図のオレンジ線
プレイヤー1 (ローブシン)
最終的に勝率9割程度まで到達。ダメ計を見るとわかるが、とびひざも大抵は珠ダメ込で耐えるので、素直にれいパン→マッパと打てば仮想プレイヤーには勝てる。

プレイヤー2 (フェローチェ)
最終勝率はMaxDamagePlayerで8割程度。
とびひざげりの命中不安があるので、9割以上は厳しいかもしれない。

プレイヤー1とプレイヤー2のどちらも、とりあえず単純な思考をする仮想プレイヤーに対して圧勝できるほどの能力は得られたことがわかった。
プレイヤー1とプレイヤー2の直接対決 (P1の勝率)
後述の戦略と合わせて見てほしいが、定期的に逆転しあっている。それでも若干P1(ローブシン)が有利なようである。
これもCFRにおいてお互いに戦略を最適化しあっていることの一つの証拠となりそうである。

結果2: 初手の戦略
前回同様に、100000回の繰り返しによって学習を行った両プレイヤーの、初手の戦略を確認する。ここでいう戦略とは各技の選択確率のことであり、どの技を選択するかは確率的に決定する。
P1 (ローブシン)
学習初期ではフェローチェのとびひざを潰す、守るを選択している。フェローチェ側がとびひざを選択しなくなると、単にダメージを稼ぐアムハンかれいパンを採用するようになる。(2つの違いはあまり学習できていない)

P2 (フェローチェ)
とびひざは守られるリスクがあるので、早々に選択確率が降下している。とりあえず身代わりで相手の珠ダメを稼ぐ戦法に落ち着いている。

結果3: 各ターンの詳細な戦略
続いて初手以外の戦略について、各ターンごとに分類して結果を記す。
なお、CFRにおいて戦略は、ゲーム木の中で情報集合ごとに蓄積・更新されている。情報集合とはそのプレイヤーが知り得る情報をグループ化したもので、ポケモンの場合であれば自分と相手の選択した行動や、急所などの確率的要素が異なるたびに、別の情報集合にたどり着いて新たに戦略を蓄積することになる。
膨大な情報集合からなるゲーム木の全体を表現することはできないので、今回は代表的な(出現回数の多い)情報集合を取り上げ、それをもとに各ターンのだいたいの戦略を記述することにする。
今回、最終(繰り返し100000回)時点では次のような流れでゲームが展開されていくことがわかった。
- ターン1: フェローチェは珠ダメを稼ぐために身代わりを選択。ローブシンは身代わりを割るためにアムハンorれいパンを選択。
- ターン2: ターン1と同様、身代わりと珠ダメージによるHP減少が行われる。
- ターン3: ローブシンはフェローチェがとびひざげりを打つことを期待して、守るを選択する。フェローチェはとびひざげり①か身代わり②を確率的に選択する。
- ターン4①: フェローチェはとびひざげりの反動ダメージでHPが極小になっているので、ローブシンがマッハパンチを打ってP1の勝ち。
- ターン4②: ローブシンはとびひざげりを防ぐまもるを打つことができず、身代わりの残ったフェローチェを一撃で倒すこともできず、P2の勝ち。

続いて各ターン(に代表される情報集合)の戦略のグラフを記す。
ターン1
(初手の戦略と同様)

ターン2
ローブシン側には若干アームハンマーとれいとうパンチのせめぎ合いがあるが、概ね図に示した通りの戦略。

ターン3
おそらくこのターンが今回の対面では一番重要。P2戦略でとびひざげり(青線)と身代わり(オレンジ線)が拮抗しているので、実際にどちらが選択されるかは、運次第である。
現時点ではとびひざげりの選択確率が若干高く、そのためローブシン側もとびひざげりに有利なように、まもる(赤線)を選択するような戦略になっている。
ちなみにまもるに対しては身代わりが有効だが、万が一この3回目の身代わりが割られると次のマッハパンチを耐えられない(33.9 ~ 39.9 % ダメージ)ので、フェローチェとしてもここで勝負を決めないといけないターンだったと思われる。

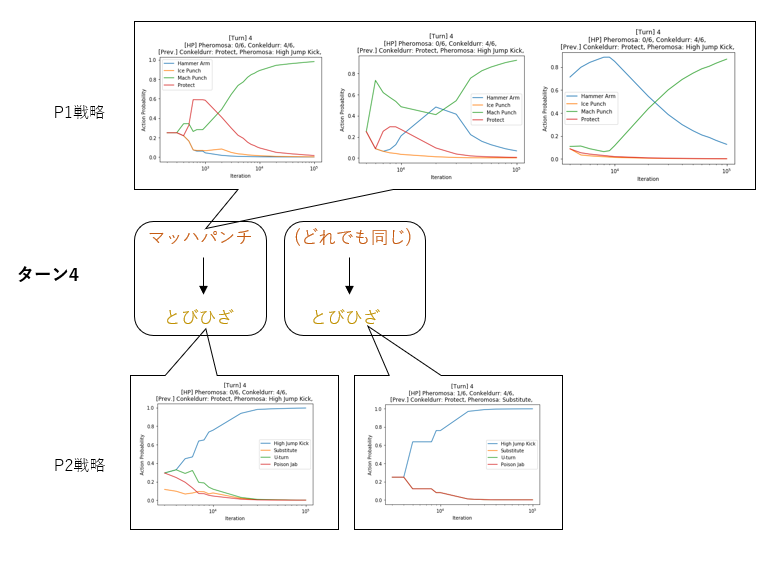
ターン4
HPの少ないフェローチェを確殺するマッハパンチ(緑線)、および珠ダメの入ったローブシンをピッタリ倒す、とびひざげり(青線)がきれいに選択されている。
結果4: 戦略の経時変化
繰り返し計算中のP1vsP2の勝率グラフを再度ご覧いただきたい。
繰り返し回数10^3ほどで、P1の勝率が大きく落ち込んでいる箇所がある。

これを考察するために、先程の詳細戦略(ターン3)のグラフで同じく10^3時点の戦略を見てみる。すると、この時点ではまだローブシン側のまもるの選択確率が低いことがわかる。

ここから繰り返し10^3=1000回時点でのだいたいの戦略を推測すると以下のようになる。つまり、フェローチェが珠ダメ2回+とびひざげりでローブシンをちょうど落とせると発見したところで、ローブシン側はその新しい戦略に対応してきれていない。結果としてとびひざげりをダイレクトに食らえばその時点でP2の勝利である。

100000回の繰り返し計算の中で、両プレイヤーの(均衡)戦略は以下のように推移していったと考えられる。
なお100000回は繰り返し回数としては少ない方で、この先もまた新たな戦略が発見されるかも?
考察・まとめ・感想
本文中に大体書いてしまった
ハッピー節分